牛顿插值法是数值分析中一种用于插值的多项式，由Issac Newton提出，是估算函数值的重要方法之一

前言

近期数值分析课程讲到了牛顿插值法，感觉比拉格朗日插值法更简单一些，出于兴趣便想用C++复现一下

GitHub地址

代码

#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
    double x[5],f[5][5],t;
    for(int i=0;i<=4;i++)
    {
        cout<<"input x"<<i<<"=";
        cin>>x[i];
        cout<<"input y"<<i<<"=";
        cin>>f[0][i];        
    }    
        cout<<"input x=";
    cin>>t;
        //输入x0-x4,y0-y4,x


    for(int i=1;i<=4;i++)
    {
        for(int j=i;j<=4;j++)
    {
        f[i][j]=(f[i-1][j]-f[i-1][j-1])/(x[j]-x[j-i]);
    }
       }
       //生成均差表


    double p=0;
    double k[5];
    k[0]=1;
    for(int i=1;i<=4;i++)
    {
        k[i]=k[i-1]*(t-x[i-1]);
    }
    for(int i=0;i<=4;i++)
    {
        p+=f[i][i]*k[i];
    }
    cout<<"p="<<p<<endl; //输出函数值p
    return 0;
}

解析

均差表的生成

均差表由一个二维数组f[][]存储

其中每项f的值为f[i][j]=(f[i-1][j]-f[i-1][j-1])/(x[j]-x[j-i])

函数P(x)的计算

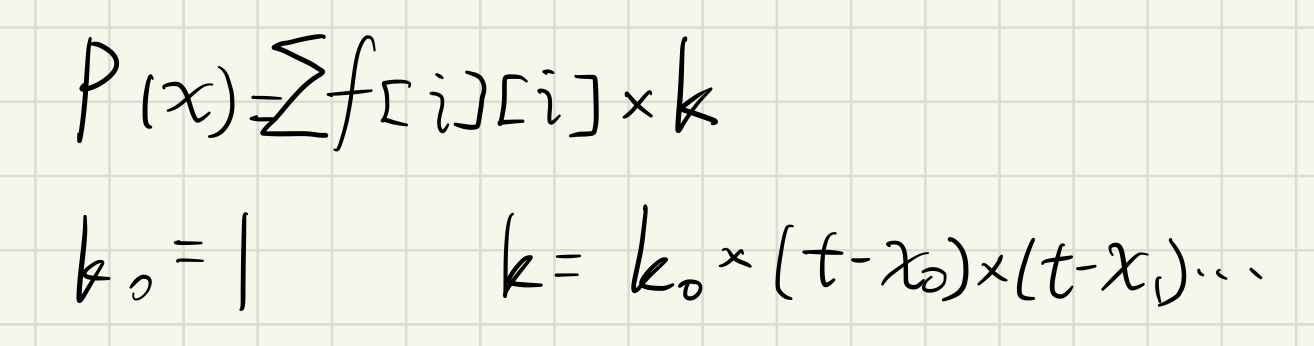
笔者在处理每项fi后面的整式时将其设为k[i]并单独计算
其中规定k[0]=1
k的生成代码为k[i]=k[i-1]*(t-x[i-1])
再规定p的初始值为0
之后使用for循环将p的值累加即可得到最终答案